In previous posts, we discussed how antenna technology is constantly evolving and how one of the main focuses of antenna design is creating powerful antennas in low-profile form factors. This is especially true for applications such as personal communications, small satellite communications, UAV communications, SIGINT and ISR.
In addition to cylindrical dipoles and biconical antennas, fractal antennas can meet the requirements of utilizing the limited available space. Fractal antennas, as the name suggests, are based on the concept of a fractal, which is a recursively generated geometry that has fractional dimensions. While fractals antennas have many complexities that can be discussed at length, in this post, we will examine the basics of fractals.

Fractal Antennas can be classified in two categories: deterministic and random.
Deterministic fractals are those that are generated of several scaled-down rotated copies o themselves. Such fractals can be generated using computer graphics that are repeatedly mapped out by a recursive algorithm. The Sierpinski gasket, for example, is a type of deterministic fractal.
Random fractals also contain elements of randomness that allow simulation of natural phenomena.
Fractal geometries can best be described and generated using an iterative process.
This process can be illustrated graphically, as shown in the illustrations of the Koch snowflake (or Koch fractal loop) and the Minkowski island fractal. The geometry generating process begins with a basic geometry known as the initiator (the triangle and the square, respectively). For Koch snowflake, the middle third of each triangle is replaced with a generator, and for the Minkowski island, each of the four sides of the square is replaced by a generator.
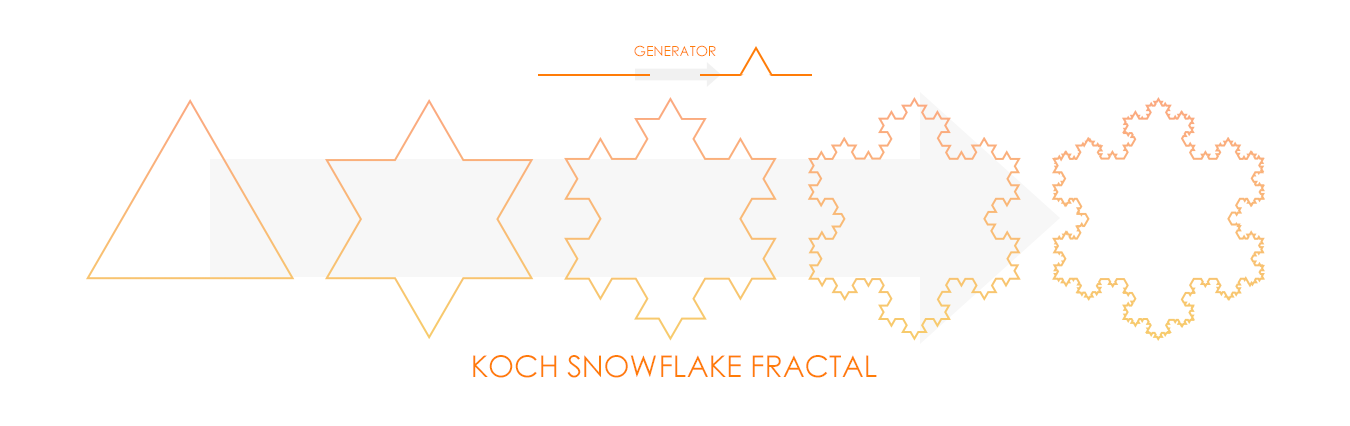
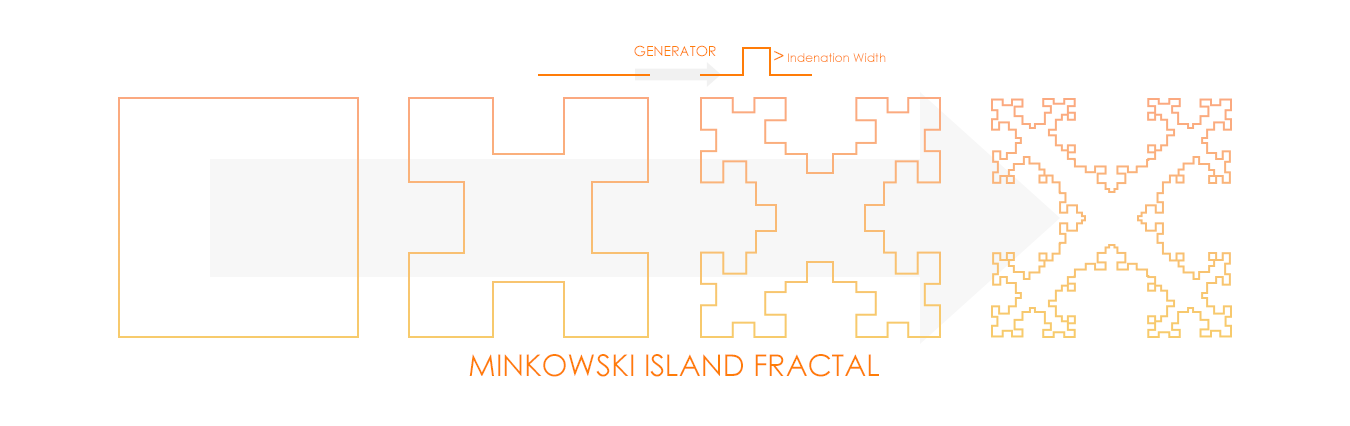
The trend of the fractal antenna geometry can be determined by observing several iterations of the process.
The final fractal geometry is a curve with an infinitely intricate underlying structure whose building blocks are scaled versions of the initiator.

Fractal antennas have space-filling properties that can be used to miniaturize classic antenna elements and overcome some of the limitations of small antennas.
Many fractal element antennas use the fractal structure as a virtual combination of capacitors and inductors. The antenna’s many resonances can vary according to the fractal design. The current on the structure has a complex arrangement caused by the inductance and self capacitance. Due to this reactive loading, the antenna elements can be compacted into a smaller space even if they are electrically long. Additionally, fractal antennas do not require additional components, assuming the structure happens to have the desired resonant input impedance.
Not all fractal antennas are ideal for certain applications.
The antenna’s suitability for a particular application can be determined by RF testing and computer search methods. Generally, the advantages of fractal antennas are good multiband performance, wide bandwidth, and small area.
While some researchers claim that fractals have superior performance, some experts claim the contrary.
In 2003, Steven R. Best wrote in A Comparison of the Resonant Properties of Small Space-Filling Fractal Antennas, “that antenna geometry alone, fractal or otherwise, does not uniquely determine the electromagnetic properties of the small antenna.” However, in 2008 Constantine A. Balanis‘s research concluded that fractal antennas performed relatively similarly to the electrically small antennas they were compared against. More recently, in 2011, authors of Small Antenna Handbook Robert C. Hansen and Robert E. Collin reviewed many papers on fractal antennas. The pair concluded that they offer no advantage over fat dipoles, loaded dipoles, or simple loops, and that “nonfractals are always better.”
Latest Posts

10 Factors that Affect Antenna Performance
We get a lot of inquiries regarding antenna performance in various settings, one of them being, “how far will the antenna propagate?” In this post, we describe some of the many factors that affect antenna performance.
Hedy Lamarr: The Hollywood Actress Who Changed Wireless Technology
This Women’s History Month, we wanted to highlight the life and career of Hedy Lamarr, a famous Hollywood star whose lesser-known achievements include essentially laying the foundations for the spectrum-hopping technology we know today as WiFi.

Living Legends: James West and Jesse Russell
Every February, JEM Engineering honors the the African American Engineers who have made lasting contributions in STEM. This year, we’re excited to spotlight two living legends: James Edward West and Jesse Eugene Russell.

11 Ways the Antenna Industry Has Changed
In this issue, we wanted to reflect upon how the antenna industry has evolved over the past several decades.

Part II: Inspecting & Testing Antennas with UAVs
In this issue, we focus on how UAVs are used for inspecting and testing antennas. Perhaps an antenna is situated in a less-accessible area.
